Tangentia
Tangentia is a term coined by one of the founders at Tangentia during its infancy in 2003 and is now a trademark owned by Tangentia Inc.
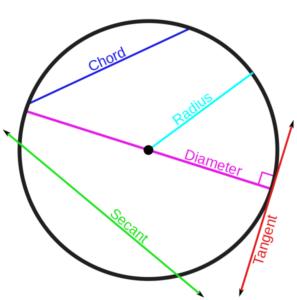
In plain English, a Tangent is a line perpendicular to the diameter of a circle and it is on the outside of the circle. So Tangentia, in our opinion, is the space around the circle.
In a business context, e.g. in a bread baking company, bread making is their core business (what is within the circle) and many critical things tangential to breadmaking that also enhances the efficiency and effectiveness of breadmaking, be it Automation, B2B Connectivity or Digital Transformation, is what Tangentia does for their business.
For the geeks reading this- here is an excerpt from Wikipedia in geometry.
Discover Our Practices
AUTOMATION
Artificial
Intelligence
Robotic Process
Automation
Blockchain
B2B CONNECTIVITY
EDI/Order
Management
eCommerce
(B2B/B2C)
Supply Chain



